มาเป็นเพื่อนกันกับอีสานเดฟ
เรารับทำและออกแบบเว็บไซต์ สำหรับธุรกิจทุกประเภท ปรึกษาฟรี !
เลขนัยสำคัญ คืออะไร

วันนี้เราจะมาพูดคุยกันถึงเรื่อง เลขนัยสำคัญ ซึ่งเป็นบทเรียนคณิตศาสตร์ที่จะเริ่มเรียนในระดับชั้นมัธยมปลาย ตอนมัธยมชั้นปีที่ 4 และสามารถนำไปสอบเข้ามหาวิทยาลัยได้ ดังนั้นจึงเป็นบทเรียนที่สำคัญมากพอดูเลย ก่อนที่เราจะอธิบายรายละเอียดในส่วนอื่นนั้น ตอนนี้เรามาดูนิยามของเลขนัยสำคัญกันก่อนดีกว่า

เลขนัยสำคัญ (significant figure) คือ จำนวนหลักของตัวเลขที่แสดงความเที่ยงตรงของปริมาณที่วัดหรือคำนวณได้ ดังนั้นตัวเลขนัยสำคัญจึงประกอบด้วยตัวเลขทุกตัวที่แสดงความแน่นอน (certainty) รวมกับตัวเลขอีกตัวหนึ่งที่แสดงความไม่แน่นอน (uncertainty) ซึ่งขึ้นอยู่กับอุปกรณ์ที่เราเลือกใช้ด้วย

จากนิยามอาจจะทำให้ดูงงไปบ้างแต่หากจะให้ว่ากันอย่างง่ายๆ นั้นตัวเลขนัยสำคัญนี้เป็นเลขที่สามารถวัดค่าได้ โดย เป็นตัวเลขที่แสดงขนาดปริมาณหรือสเกลอย่างแน่นอนโดยสามารถวัดได้จากไม้บรรทัดและวัดได้เป็นหน่วยที่เล็กที่สุดของไม้บรรทัดหรือของเครื่องมืออื่น โดยเลขนัยสำคัญนี้สามารถนำไปบวกลบคูณหารทางคณิตศาสตร์ได้ตามปกติ
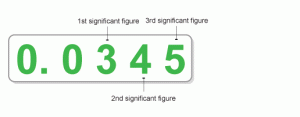
โดยเราจำต้องจำตัวเลขที่เป็นกฎของเลขนัยสำคัญกันให้ได้ก่อนโดยเลขที่จะสามารถเป็นเลขนัยสำคัญได้จะมีอยู่ 5 ข้อด้วยกัน
- ตัวเลขที่ไม่ใช่ 0 (ศูนย์) เป็นเลขนัยสำคัญ เช่น
321, 456.43, 947, 8889
- เลข 0 (ศูนย์) ที่อยู่ระหว่างตัวเลขถือเป็นเลขนัยสำคัญ เช่น
909, 75408, 58.505, 1001
- เลข 0 (ศูนย์) ที่อยู่ทางซ้ายของตัวเลขที่ไม่ใช่ศูนย์ ไม่ถือเป็นเลขนัยสำคัญ จุดมุ่งหมายก็เพื่อแสดงตำแหน่งของจุดทศนิยม เช่น
0.00055 มีเลขนัยสำคัญ 2 ตัว
0.0594 มีเลขนัยสำคัญ 3 ตัว
0.0000004847477 มีเลขนัยสำคัญ 7 ตัว
โดยศูนย์ที่อยู่ทางซ้ายไม่ถือว่าเป็นเลขนัยสำคัญ
- เมื่อตัวเลขมีค่ามากกว่า 1 เลข 0 (ศูนย์) ที่เขียนทางขวามือถือเป็นเลขนัยสำคัญ เช่น
0.0000809800 มีเลขนัยสำคัญ 6 ตัว 45.500 มีเลขนัยสำคัญ 5 ตัว 140.0 มีเลขนัยสำคัญ 4 ตัว
- แต่ถ้าตัวเลขมีค่าน้อยกว่า 1 เลข 0 (ศูนย์) ที่อยู่ท้ายตัวเลขและอยู่ระหว่างตัวเลขถือเป็นเลขนัยสำคัญ เช่น
0.040 มีเลขนัยสำคัญ 2 ตัว 0.2005 มีเลขนัยสำคัญ 4 ตัว 0.000136 มีเลขนัยสำคัญ 3 ตัว
การคำนวณเลขนัยสำคัญโดยปกติและจะมีวิธีการดังนี้
- การคำนวณด้วยวิธีการบวกและลบจำเป็นจะต้องทำให้หลักของเลขเท่ากับข้อมูลที่มีเลขทศนิยมน้อยที่สุด
2.เช่นเดียวกับการบวกและลบ การคูณและหารก็จำเป็นจะต้องทำให้หลักของเลขเท่ากับข้อมูลที่มีเลขทศนิยมน้อยที่สุด
การระบุจำนวนเลขนัยสำคัญของผลลัพธ์ที่ได้จากการคำนวณ
มีวิธีการดังนี้
1 ผลลัพธ์จากการบวกและลบ ต้องมีจำนวนเลขทศนิยมเท่ากับข้อมูลที่มีเลขทศนิยมน้อยที่สุด
เช่น 123.653 + 0.33 +22.5614 = 146.5444 บันทึกเป็น 146.54
2 ผลลัพธ์จากการคูณและหาร ต้องมีจำนวนเลขนัยสำคัญเท่ากับข้อมูลที่เลขนัยสำคัญน้อยที่สุด
เช่น 25 × 2.45 ÷ 100 = 0.6125 บันทึกเป็น 0.61
3 ข้อมูลที่มาจากการนับหรือการเทียบหน่วยในระบบเดียวกัน ไม่นำมาพิจารณาจำนวนเลขนัยสำคัญ หรือข้อมูลอันเกิดจากการเทียบหน่วยจะไม่ถูกนำมานับเช่น เมตรเมื่อเทียบกับเซนติเมตร กรัมเมื่อเทียบกับกิโลกรัมนั้นเอง
สำหรับข้อมูลในวันนี้นั้นเป็นข้อมูลพื้นฐานของเรื่องเลขนัยสำคัญ ที่จำเป็นในการใช้งานและเรียนรู้ในเบื้องต้น อย่างไรก็ดี หากข้อมูลนี้มีประโยชน์ต่อผู้อ่านก็คงจะเป็นเรื่องที่ดีนะคะ
ในโอกาสหน้าครั้งถัดไปเราจะนำอะไรมาฝากอีกนั้นรอติดตามกันนะคะ
